| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- 코틀린
- ML
- 경쟁 조건
- cross_val_score
- min-max
- 멀티 프로그래밍
- jdk #javac #jre #java standard library #javadoc #jar #java
- 결정트리
- featureimportances
- 11049
- 디자인 패턴 #싱글톤
- 속성중요도
- 운영체제
- 머신러닝 #ml #기본기
- bootstrapping
- JetBrains
- 머신러닝 #ml #선형대수학 #기본기
- featurescaling
- Java
- 머신러닝 #ml #미분 #기본기
- Mutex lock
- ml
- db
- Kotlin
- 에다 부스트
- 지니불순도
- 상호 배제
- gridsearch
- 다항회귀
- Mutual exclusion
- Today
- Total
코딩하는 오리
[ML] 기본 지도 학습 알고리즘들 - 4. 로지스틱 회귀 (Logistic Regression) 본문
01. 분류 문제
머신러닝 : 지도학습 vs 비지도학습
지도학습 : 회귀 vs 분류
분류 : 정해진 몇 개의 값 중에 예측(0, 1, 2)
이를 선형 회귀를 통해서 분류한다면 0.5 이상이면 통과, 아니면 탈락으로 예측 가능

이렇게 간단하지만, 우리는 분류에 선형 회귀를 잘 사용하지 않는다.
Why?
예를들어서 10000시간 공부한 데이터가 추가되었을 경우 이 하나의 데이터로 인해 그래프가 더 눕는다.
이로 인해 통과 지점이 100시간 이상에서 200시간 이상으로 변해버림
선형 회귀는 예외적인 데이터에 민감하여 분류 할 때는 잘 사용하지 X

03. 로지스틱 회귀 (Logitstic Regression)
선형 회귀는 데이터에 잘 맞는 1차 함수를 찾는것이라면
로지스틱 회귀는 데이터에 잘 맞는 시그모이드 함수를 찾는 것
시그모이드 함수는 반드시 0과 1 사이의 결과 값 도출

* 선형 회귀는 결과가 범위 없이 얼마든지 크거나 작아질 수 있음
* 무조건 0과 1 사이의 값이 나오는 시그모이드 함수가 분류에 더 적합 !
로지스틱 회귀는 분류에 쓰이는데 왜 회귀 ? 결과값이 연속적이기 때문
주로 0.5보다 크지 작은지로 분류하게 될 것

05. 로지스틱 회귀 가설함수
가설함수 : 입력 변수를 받아서 목표 변수를 예측해주는 함수

07. 로지스틱 회귀에서 하려는 것

08. 결정 경계
Decision Boundary : 분류할 때 분류를 구별하는 경계선

09. 로그 손실
가설함수를 평가하는 기준 : 손실 함수
선형회귀의 손실함수 : 평균 제곱 오차의 개념 기반
로지스틱 회귀의 손실함수는 로그 손실(log-loss / cross entropy) 사용


y=1 : h(x)가 0.8이면 80%의 확률로 아웃풋이 1일 것이라고 예측하는 것. 실제 결과가 1이기 때문에 이 가설함수는 꽤 잘 했다고 평가 가능(손실이 있지만 크지는 않다). 하지만 왼쪽으로 갈수록 손실이 커지는데 1에서 멀어질 수록 손실을 급격히 키워준다
y=0 : h(x)가 0.2라면 20%의 확률로 아웃풋이 1일 것이라고 예측하는 것. 실제 결과가 0이기 떄문에 꽤 잘했다고 평가 가능.
손실의 정도를 로그 함수로 결정하기 때문에 로그 손실 !
11. 로지스틱 회귀 손실 함수
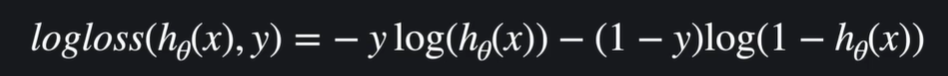
회귀 손실함수 : 모든 데이터의 로그 손실을 계산한 후, 평균을 낸다. input은 세
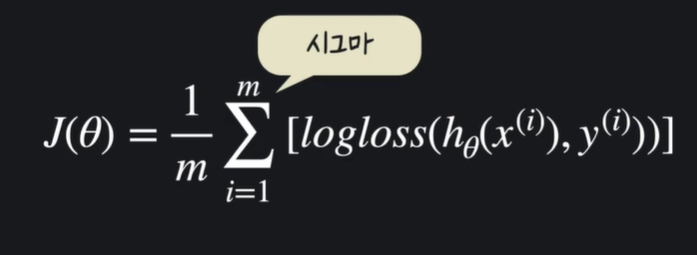
13. 로지스틱 회귀 경사 하강법
손실을 최소화하는 것이 목표 !
경사하강법은 손실을 최소화하는 하나의 방법
로지스틱 회귀의 경사하강법은 선형 회귀와 비슷하다.
임의의 세타 값에서 시작하여 세타 값을 업데이트 하며 손실을 최소화

경사하강법에서는 항상 세타 값으로 미분한다.

15. 로지스틱 회귀 구현하기 쉽게 표현하기
선형회귀와 동일하게 ~

가설함수 = sigmoid(X@세타)

18. 분류가 3개 이상일 때
지금까지는 분류 옵션이 2가지
만약 이메일을 3가지 옵션으로 분류하려면 ?
각 옵션에 0, 1, 2 값을 지정
처음에는 0인지, 0이 아닌지에 대해 분류한다.
그 다음에는 1인지, 1이 아닌지 분류한다.
마지막으로 2인지, 2가 아닌지 분류한다.
각각의 옵션에 대해 가설함수를 입력한다.

각각의 가설함수 결과 스팸 메일 확률 값이 가장 크기 때문에 스팸 메일로 분류 하면 된다 !
20. 로지스틱 회귀와 정규 방정식
로지스틱 회귀에서는 정규 방정식과 같은 단순 행렬 연산만으로는 손실함수의 최소 지점을 찾을 수 없다.
선형 회귀는 손실함수 J(MSE)가 convex(아래로 볼록)할 뿐만 아니라, 편미분 원소들을 모두 선형식으로 나타낼 수 있었기 때문에 가능.
로지스틱 회귀에서는 손실함수 J(로그 손실)가 아래로 볼록하다(convex). 따라서 경사하강법을 이용하면 항상 최적의 세타 값들을 찾을 수 있다.
하지만, J에 대한 편미분 원소들이 선형식이 아니다. 가장 기본적으로 세타가 e의 지수에 포함되었는데 지수로 포함된 식은 일차식으로만 표현하기가 불가능하다. 따라서 단순 행렬만으로는 최소 지점을 찾아낼 수 없다..
21. scikit-learn 로지스틱 회귀 데이터 준비
from sklearn.datasets import load_iris
iris_data = load_iris()
iris_data.DESCR - 붓꽃의 종류를 분류하는 것 !
X = pd.DataFrame(iris_data.data, columns = iris_data.feature_names)
y = pd.DataFrame(iris_data.target, columns = ['class'])
22. scikit-learn으로 로지스틱 회귀 쉽게하기
from sklearn.linear_model import LogisticRegression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
y_train = y_train.values.ravel()
model = LogisticRegression(solver='saga', max_iter='2000') : 사용 알고리즘은 saga, 최대 반복횟수는 2000으로 설정(더 빨리 최적화되면 그 앞 iter에서 중단한다)
model.fit(X_train, y_train)
model.predict(X_test)
model.score(X_test. y_test)

'AI > ML' 카테고리의 다른 글
| [ML] 결정 트리와 앙상블 기법 - 2. 랜덤 포레스트 (Random Forest) (0) | 2024.07.31 |
|---|---|
| [ML] 결정 트리와 앙상블 기법 - 1. 결정 트리(Decision Tree) (0) | 2024.07.30 |
| [ML] 기본 지도 학습 알고리즘들 - 3. 다항 회귀 (Polynomial Regression) (0) | 2024.07.30 |
| [ML] 기본 지도 학습 알고리즘들 - 2. 다중 선형 회귀(Multiple Linear Regression) (0) | 2024.07.29 |
| [ML] 기본 지도 학습 알고리즘들 - 1. 선형 회귀(Linear Regression) (0) | 2024.07.27 |




