[ML] 기본 지도 학습 알고리즘들 - 2. 다중 선형 회귀(Multiple Linear Regression)

01. 다중 선형 회귀

 

일반적으로는 여러 입력 변수를 가지고 선형 회귀 진행한다.

입력변수가 1개 일 경우 시각적으로 표현하기 쉬웠음.

그러나 다중 선형 회귀는 시각적으로 표현 어려움

 

BUT 시각화만 못 할 뿐, 기본 개념은 Linear Regression과 동일

 

02. 다중 선형 회귀 표현법

입력 변수 : 여러 개(속성 - feature) 

목표 변수 : 1개

 

 

 

04. 다중 선형 회귀 가설함수

항이 많을 뿐 1차 함수~

 

 

06. 다중 선형 회귀 경사 하강법

선형 회귀와 동일～똑같은데 단지 세타 값이 많을 뿐

동일하게 손실함수 사용. 손실함수는 세타 값에 대한 함수 

어떤 세타 값을 쓰냐느냐에 따라 손실함수의 값 달라짐

 

최대한 손실함수의 값을 작게 만들자

경사하강법 사용 ： 손실을 가장 빨리 줄이는 방향으로 세타 값을 바꿔주는 방법

 

11. 정규 방정식(Normal Equation)

 

경사하강법은 조금씩 손실함수의 극솟값에 도달하는데

기울기가 0 인 지점을 찾도록 정규방정식을 통해서도 손실함수 찾을 수 있다.

 

정규방정식 계산하는 방법

 

14. 경사 하강법 vs 정규 방정식

 

경사 하강법 : 적절한 학습률 알파를 찾아야한다. 반복문 사용해야 한다. 입력변수 n이 커도 효율적 연산 가능

정규 방정식 : 학습율 알파 필요X. 한 단계로 계산 가능. 입력변수 n이 커지면 월등히 비효율적. 역행렬일 존재하지 않을 수도 있음

 

 

절대적으로 정해진 것은 없으나

입력변수의 수가 엄청 많을 때(1000개 이상)이면 경사 하강법, 비교적 입력 변수 수 적을 때 정규 방정식 사용.

 

15. Convex 함수

 

손실함수 J의 경사를 구한 뒤 이걸 이용해서 최솟값을 갖는 세타를 찾았습니다.

하지만 단순히 경사 하강법과 정규방정식만 이용하면 항상 손실 함수의 최소 지점을 찾을 수 있을까 ?

 

만약 이런 함수에서 경사 하강법을 적용한다면

쭉 내려가다 극소값 중 하나에 도달하면 경사가 0이어서 경사 하강이 종료가 되지만, 손실함수의 최저점은 찾을 수 없다.

 

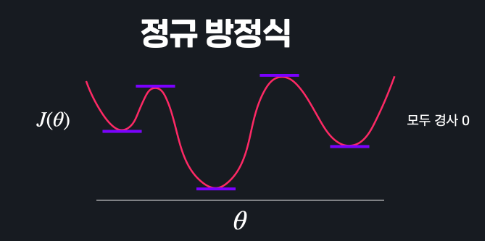
정규 방정식도 마찬가지. 수많은 극소, 극대값들이 있으면 아무리 방정식을 해결해도 수많은 지점 중 어떤 지점이 최소점인지 알 수 가 없다. 

 

Convex 함수(아래로 볼록한 함수) 는 어떤 지점에서 경사하강을 시작해도 항상 손실 함수의 최소지점을 찾을 수 있고, 정규방정식도 이용 가능하다.

 

그 위의 함수는 non-convex 함수

 

선형 회귀의 평균 제곱 오차

 

선형 회귀에서는 가정함수의 예측값과, 실제 목표 변수들의 평균 제곱 오차(MSE)를 손실함수로 사용해쓴데

다행히 MSE는 항상 convex 함수.

따라서 선형 회귀 할 때는 경사 하강법, 정규 방정식으로 항상 최적의 세타 찾기 가능

 

 

17. scikit-learn으로 다중 선형 회귀 쉽게 하기

- 선형 회귀와 거의 동일

- coef 값에는 세타 1 ~ 여러 값이 담겨있음

- 최종 MSE 구했을 때 약 4500 달러 오차 발생. 선형 회귀인 약 8000 달러 오차 보다 더 정확한 결과